Paper Notes # 3 Learning Group Structure and Disentangled Representations of Dynamical Environments

What?

This work proposes a method to learn the symmetries of a dynamical environment without supervision and prior information of such symmetries.

Why?

In such a representation agent can associate simple actions to distinct subspaces and compose actions to form complex maniputations. They are also appealing from robustness and interpretebility perspective.

How?

To learn a representation of the environment, the observations in space X are mapped to the latent space V with f: X \rightarrow V. Similarly, the transformations g \in G are represented by linearly acting matrices on V. Their method assumes that all transformations in the unknown symmetry group G of the envoriment can be represented by linear transformations in V. Specifically, linear trasnforms are identified with (special orthogonal) matrices belonging to SO(n) i.e. set of orthogonal n \times n matrices that act linearly on the latent space.

This gives the following relationship: f(g \cdot x_1) = \rho(g) \cdot f(x_1) . That is, if we first transform x_1 with g and encode it. This should be same as first encoding x_1 and then transforming this representation with g‘s representation. This is another way of saying that we can capture real-world manipulations via (learned) trasnformations of space in our (learned) representation.

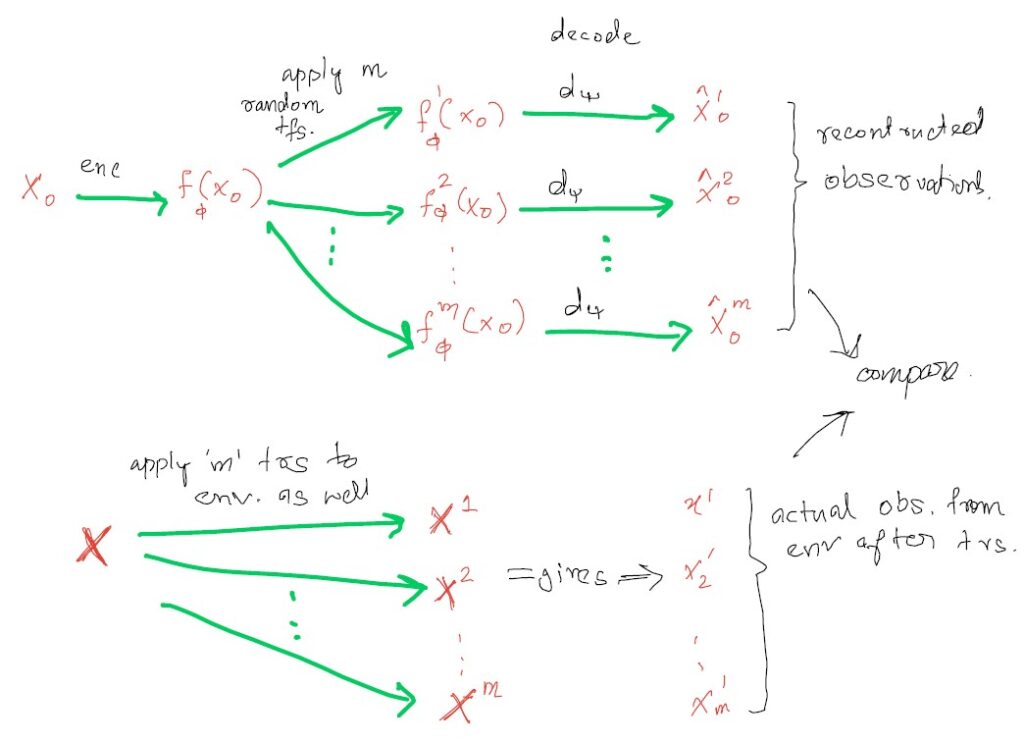
Representation: Parameterize the n dimensional representation of any transformation g as product of n(n-1)/2 rotations with params \theta where \theta_{i,j} is the rotation in i,j plane embedded in n dimensional representation. “Parameters \theta, are learned jointly with the parameters of an encoder f_{\phi} mapping the observations to the n-dimensional latent space and a decoder d_{\psi} mapping the latent space to observations. Both encoder and decoder can be implemented as Nerual Netwroks.

Training procedure: Encode a random observation x_0 with f_{\phi} then transform the environment and the latent vector f_{\phi}(x_0) using m random transformations and their representation matrices \{g_{k}\}_{k=1}^m. The result of those linear transformations in the latent space is decoded with d_{\psi} and yields \hat x_m. The training objective is to minimize the reconstruction loss L(\phi, \psi, \theta) between actual observations x_m and reconstructed \hat x_m.

And?

• For disentanglement we want each subgroup of symmetry group to act only on specific subspace of latent space. That is if we want each trasnformation to act on a minimum of dimensions of latent space.
• They include several examples where the method recovers unknown symmetries in2D and 3D case.
• I don’t quite understand why they apply m transformations.