Paper Notes # 2 Towards A Definition of Disentangled Representations

What?

Models use an internal representation which encodes information about the state of the world. We would like such a representation to be robust to the changes in parts of the world such that only the part of representation relevant to that change is affected. Such a represenation is called a “disentangled representation“. The concept is fairly intuitive and useful; however, there has been no widely accepted definiton of what “disentangled representation” actually is. This paper aims to address this.

Why?

Disentangled representations can provide many desirable properties such as (1) Modularity (2) Compactness: (3) Explicitness.

How?

“By connecting symmetry transformations to vector representations using the formalism of group and representation theory we arrive at the first formal definition of disentangled representations”

From paper abstract

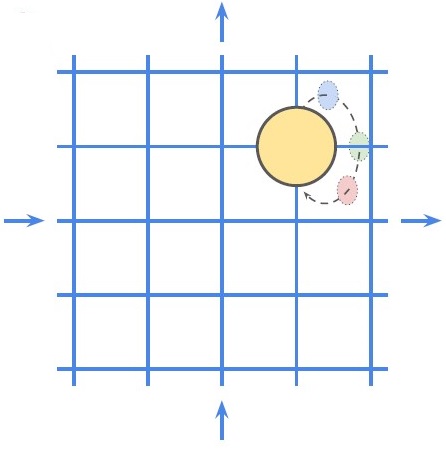
World dynamics can be described in terms of symmetry transformations that change certain aspects of the world state while keeping other aspects unchanged. For example, changing color or position of the ball.

We need to following ingredients for the formalism:

A generative process: b : W \rightarrow O , an inference process which converts our observations into an internal representation h : O \rightarrow Z , and finally a composition f : W \rightarrow Z where f = h \circ b (i.e. mapping from world to our representation)

Symmetry (transformation): A transformation which leaves certain properties of the object invariant. In above example, a circle translated or with a different color is still a circle.

Symmetry group: Set of symmetry transformations. In this example we have \{ \text{x-translation}, \text{y-translation}, \text{color-change} \}

Action (of symmetry group): Effect of symmetry transformation on the state of the world.

Disentangled group actions: Actions which change a certian aspect of the world state while keeping others fixed. For example, a change in color without affecting position.

With this in place, we want to find a mapping between the disentangled group action in the abstract state space and the transformations in the vector space of representations, so that the latter reflect the structure of the former. If such a mapping exists, then it produces a disentangled representation. Intuitively, we define a vector representation as disentangled, if it can be decomposed into a number of subspaces, each one of which is compatible with, and can be transformed independently by a unique symmetry transformation. How the transformation has to be parameterized is not discussed in this work.

And?

• Rotations about the different axes do not commute with one another, and hence the group of symmetries does not decompose in the way that we might intuitively hope.
• Group decompositions can be discovered empirically through active perception. By acting in the world, agents should be able to discover which aspects of the world remain invariant under various transformations. This is almost the same as distributional robustness criterion.
• A symmetry group may have different subgroup decompositions. It has to be assumed that the structure of the world dictates a certain natural decomposition (e.g. via known generative factors or causal graph).